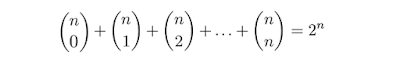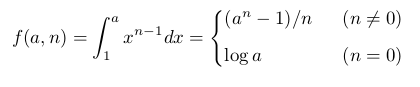Matematiğin faydasından çok güzelliğini vurgulayan bu sayfalarda bir düzine ilginç konu bulacaksınız. Matematikçi, yaptığı işin faydasını ve uygulamasını asla düşünmez. Onun için en önemli motivasyon, gizli kalmış hakikatleri gün ışığına çıkartmaktan ibaret. Daha sonra diğer bilimlerde ya da mühendislikte uygulama alanı bulunursa ne ala... Bulunmazsa da matematikçinin umurunda değil...
Konuları seçerken, Marmara Üniversitesinde 2008-2016 arasında verdiğim IE 701 (Engineering Mathematics) doktora dersinin muhtevasını kullandım. Dersin önemli özelliği, haftalık ödevlerle bu hakikatleri öğrencinin tekrar keşfetmesini sağlamak oldu. Dersimiz mühendislik kodlu olduğu için, uygulama alanı bulunan konulara ağırlık verdik. Dersin yaklaşık üçte birini bu konular kaplıyordu.
Bu sayfalarda verilen kanıtlar, bir matematikçinin aradığı titizlik ve katılıktan uzak. Buna rağmen, arka planda doğruluğu şüphesiz olan hakikatlerin neden doğru olduğunu meraklı okuyucuya anlatıyor.
Öte yandan, bu konuların hiçbiri okuyup geçilecek hafiflikte değil. Ciddi bir matematik okuyucusu kağıt kalem ile şekilleri çizmeli, formülleri türetmelidir. Bununla yetinmeyip, verilen kanıtları sayılarla doğrulamalıdır. Ancak o zaman konuyu anlamak yönünde ilerlemiş olur.
Haftalık Konu Listesi
Introduction and Proportion
Similarity and The Golden Mean
Graphs and Maps
Polyhedra: Platonic Solids
Transformation of the Platonic Solids
Uniform Polyhedra
(Midterm)
Natural and Rational Numbers
Complex Numbers: FT of algebra
Functions and Limits
Calculus: Integral and Derivative
Fundamental theorem of calculus
Computational complexity
NP-completeness
Referans
Söz konusu derste iki kitap kullandık:
1) J Kappraff, Connections: The Geometric Bridge Between Art and Science, 1991
Dersin geometri ağırlıklı ilk yarısında, şekiller ve simetri çalışırken, Connections temel kaynağımız oldu.
2) R Courant, H Robbins, What Is Mathematics? 1941
Sayılar ve forksiyonlar ile uğraşan analiz ağırlıklı ikinci yarıda da bu kitap temelimiz oldu.
2.07.2017
1.07.2017
Pisagor Teoremi
Ortaokul yaşlarında öğrenip de hayran kaldığım bu hakikatin neden doğru olduğunu o zaman çok merak etmiştim. Meğer yüzlerce ispatı varmış. Penrose bunlardan ikisini öyle vermiş ki, tekrar hayrete düştüm, yeniden hayran kaldım. Bir bilmece ile başlayalım: Farklı boyda iki kare verilmiş, bunları düz çizgilerle kesip yeniden düzenleyerek büyük bir tek kare yapabilir misiniz? Aşağıdaki şekil, bunun nasıl olacağını kolayca gösteriyor:
Büyük kare üstünde a uzunluğunu işaretledikten sonra, iki kareyi yan yana koyalım. Birbirine dik iki darbe ile kareleri beş parçaya bölelim. Üç parçanın yerini değiştirerek büyük kare kolayca elde edilir.
En sağdaki üçgenin kenarları arasında a² + b² = c² eşitliğini göstermiş olduk. 2500 sene önce İyonya'da yaşamış Pisagor'un adını taşıyan bu teoremin yüzlerce ispatından en güzel ve basit beş tanesini buraya aldım.
Teoremin cebir-geometri karışık ispatları pek hoştur:
Soldaki şekilde, her üçgenin alanı ab/2 olduğundan, (a+b)² − 2ab = c² ifadesi bir hamlede sonuca ulaşıyor. Sağda ise, (b−a)² + 2ab = c² eşitliği aynı sonucu veriyor.
Penrose'un verdiği ilk kanıt sadece geometri kullanıyor, cebir yok:
İki üçgeni ötelemek yeter, ne sayı ne de söz gerekiyor...
Benzer Üçgenler
Pisagor teoreminin en çarpıcı kanıtları benzerlik üstüne kurulmuş:
Düşey çizginin ayırdığı iki üçgenle, asıl üçgenin benzerliği çok açık.
Küçük üçgende p/a = a/c ==> a² = pc
Büyük üçgende q/b = b/c ==> b² = qc
İki tarafı toplayıp c = p+q olduğunu görmek yeterli.
Penrose'un verdiği ikinci kanıt da aynı benzerliği kullanıyor. Şekildeki üç üçgen benzer olduğu için, her birinin alanı uzun kenarının karesi ile orantılı. Üçgenlerin alanları S1 + S2 = S olduğundan, a² + b² = c².
Geometrik Kanıt
Buraya aldığım ispatları Euclid beğenip de kitabına koymazdı. Çünkü hiçbiri temel aksiyomlara kadar inen bir mantık zinciri değil. Pisagor'dan 250 yıl sonra yazılan Elements isimli geometri kitabında temellere dayanan ispatı basitleştirerek buraya alalım:
Şekildeki mavi ve sarı üçgenler eşit. Sarı üçgenin alanı, karenin alanının yarısı: a²/2. Mavi üçgen ise soldaki dikdörtgenin yarısı, yani o da a². Aynı şekilde, sağdaki dikdörtgenin alanı b² olduğuna göre, a² + b² = c² bulunur.
Ödev
a²+b²+c² = d² denklemine tamsayılı çözümler bulun
Referans
Bu yazının aslı, 2007 yılında İki Kareden Tek Kareye olarak yayınlanmıştı
Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, 2004
Pythagorean theorem:
Wikipedia
Mathworld
Mathsisfun
Cut-the-knot
Büyük kare üstünde a uzunluğunu işaretledikten sonra, iki kareyi yan yana koyalım. Birbirine dik iki darbe ile kareleri beş parçaya bölelim. Üç parçanın yerini değiştirerek büyük kare kolayca elde edilir.
En sağdaki üçgenin kenarları arasında a² + b² = c² eşitliğini göstermiş olduk. 2500 sene önce İyonya'da yaşamış Pisagor'un adını taşıyan bu teoremin yüzlerce ispatından en güzel ve basit beş tanesini buraya aldım.
Teoremin cebir-geometri karışık ispatları pek hoştur:
Soldaki şekilde, her üçgenin alanı ab/2 olduğundan, (a+b)² − 2ab = c² ifadesi bir hamlede sonuca ulaşıyor. Sağda ise, (b−a)² + 2ab = c² eşitliği aynı sonucu veriyor.
Penrose'un verdiği ilk kanıt sadece geometri kullanıyor, cebir yok:
İki üçgeni ötelemek yeter, ne sayı ne de söz gerekiyor...
Benzer Üçgenler
Pisagor teoreminin en çarpıcı kanıtları benzerlik üstüne kurulmuş:
Düşey çizginin ayırdığı iki üçgenle, asıl üçgenin benzerliği çok açık.
Küçük üçgende p/a = a/c ==> a² = pc
Büyük üçgende q/b = b/c ==> b² = qc
İki tarafı toplayıp c = p+q olduğunu görmek yeterli.
Penrose'un verdiği ikinci kanıt da aynı benzerliği kullanıyor. Şekildeki üç üçgen benzer olduğu için, her birinin alanı uzun kenarının karesi ile orantılı. Üçgenlerin alanları S1 + S2 = S olduğundan, a² + b² = c².
Geometrik Kanıt
Buraya aldığım ispatları Euclid beğenip de kitabına koymazdı. Çünkü hiçbiri temel aksiyomlara kadar inen bir mantık zinciri değil. Pisagor'dan 250 yıl sonra yazılan Elements isimli geometri kitabında temellere dayanan ispatı basitleştirerek buraya alalım:
Şekildeki mavi ve sarı üçgenler eşit. Sarı üçgenin alanı, karenin alanının yarısı: a²/2. Mavi üçgen ise soldaki dikdörtgenin yarısı, yani o da a². Aynı şekilde, sağdaki dikdörtgenin alanı b² olduğuna göre, a² + b² = c² bulunur.
a²+b²+c² = d² denklemine tamsayılı çözümler bulun
Referans
Bu yazının aslı, 2007 yılında İki Kareden Tek Kareye olarak yayınlanmıştı
Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, 2004
Pythagorean theorem:
Wikipedia
Mathworld
Mathsisfun
Cut-the-knot
Üçgenin Alanı
Üçgenin alan formülünü herkes bilir: ch/2, yani taban çarpı yükseklik bölü iki, bunun için ayrı bir konu açmaya değer mi?
Ya yüksekliği bilmiyorsak? Günlük hayatta karşımıza çıkan üçgenlerin kenarlarını kolayca ölçebiliriz, ama arazide yatay bir yüksekliği ölçmek hiç kolay değil.
Mesela, kenarları 17, 25 ve 28 metre olan üçgenin alanı nedir? Bu sorunun cevabı Euclid'de değil, ondan birkaç yüz sene sonra yaşamış olan Heron'un formülünde:
Alan² = (a+b+c)(b+c−a)(a+c−b)(a+b−c)/16
= (17+25+28)(25+28−17)(17+28−25)(17+25−28)/16 = 44100
h² terimlerini eşitleyince
289 − p² = 625 − 784 + 56p − p²
56p = 448 ve p = 8 bulunur.
Buradan h² = 17² − 8² = 225
h = 15 ve Alan = ch/2 = 210 sonucuna ulaştık.
Genelleme
Verilen üç uzunluk için, iki denklemle alanı hesaplamayı başardık. Peki bu hesabı a, b, c kenar uzunlukları için genelleyen Heron formülüne nasıl ulaşacağız?
h² terimlerini eşitleyince
a² − p² = b² − c² + 2cp − p²
Buradan 2cp = a² − b² + c²
ve p = (a² − b² + c²)/2c bulunur.
[Bu noktada bir nefes alıp p = a cos B olduğunu hatırlarsak, B açısı için kosinüs kuralı yan ürün olarak karşımıza çıkıyor: cos B = (a² − b² + c²)/2ac ]
Öte yandan, iki kare farkını kullanarak, bilinmeyen ifadeyi bir çarpım olarak yazabiliriz:
h² = a² − p² = (a+p)(a−p)
İki kare farkını bir daha kullanalım:
(a+p) = ((a+c)²−b²)/2c = (a+c+b)(a+c−b)/2c
Diğer çarpan da benzer şekilde şöyle hesaplanır:
(a−p) = (b²−(a−c)²)/2c = (b+a−c)(b−a+c)/2c
Bu iki ifadenin çarpımından h², onun c²/4 ile çarpımından alanın karesi bulunur:
Alan² = c²h²/4 = (a+b+c)(b+c−a)(a+c−b)(a+b−c)/16
Heron formülünün bilinen şekline ulaşmak için üçgenin yarı çevresini tanımlayalım:
2s = (a+b+c)
Bu ifadeden sıra ile 2a, 2b, 2c çıkartınca
2(s−a) = (b+c−a)
2(s−b) = (a+c−b)
2(s−c) = (a+b−c) bulunur.
Böylece Alan² = s(s−a)(s−b)(s−c) elde edilir.
Geometrik Kanıt
Bu hesap Heron zamanında yapılamazdı, çünkü cebirsel ifadeler henüz bilinmiyordu. Euclid'in yaptığı gibi, sadece uzunluklar ve oranlar kullanan geometrik bir kanıt gerekiyordu. Öncelikle açıortayların kesiştiği noktayı merkez alan iç çemberi çizelim:
Kenar uzunlukları yerine α, β, γ teğet uzunlukları kullanalım:
α+β=28, γ+α=25, β+γ=17 denklemlerinden α=18, β=10, γ=7 bulunur.
Çemberin yarıçapı r bilinirse Alan = αr+βr+γr = sr olarak hesaplanır.
Şekilde boyalı üç merkez açının toplamının π radyan (180 derece) olduğunu not edelim, 3. ödevde gerekecek.
Heron'un karmaşık kanıtını anlamak için B'nin açıortayına çizilen dikme ile c kenarına çizilen dikmeyi H noktasında kesiştirelim ve ortaya çıkan sarı ve mavi üçgenlerde benzerlik arayalım:
Sarı üçgenin benzerliğinden, şekilde yazılı ilk iki orantıyı görmek kolay. Üçüncü orantı için gereken mavi üçgenlerin benzerliğini kanıtlamak biraz daha zor, yukarıda not edilen ipucu ile, HB çaplı çemberin A'dan geçtiğini düşünmek gerekecek.
Cebir kullansaydık, üç bilinmeyenli üç denklem kolayca çözülürdü. Ama cebir bilmeyince aynı işi üçgenler ve orantılarla yapmak gerekiyor!
Son iki eşitlikteki u/r oranını (18−t)/t = 28/7 şeklinde birleştirince, sadece t bilinmeyeni kalır. Paydaları paylara ekleyince orantının bozulmayacağını Heron iyi biliyordu.
Buradan 18/t = 5 ya da t = 18/5 ve ilk orantıdan r² = 10t = 36 olarak bulunur.
Daha önce bulduğumuz gibi, Alan = sr = 35x6 = 210 sonucuna ulaştık. Bu yöntemin genellemesini meraklı okuyucuya bırakıyorum.
Ödev
1. Kenar uzunlukları 15, 20, 25 cm olan üçgenin alanını her iki yöntemle hesaplayın.
2. Alanın tamsayı olduğu başka a, b, c tamsayıları bulabilir misiniz?
wikiwand.com/en/Heronian_triangle
3. Kenarları √2, 2, √10 olan üçgenin alanını formül ile hesaplayın ve temel geometri bilginizle sonucu doğrulayın.
4. Şekildeki mavi üçgenlerin benzerliğini gösterin.
5. Son hesabı genelleştirerek r² = αβγ/s ve
Alan² = sαβγ = s(s−a)(s−b)(s−c) olduğunu gösterin.
Referans
William Dunham, Journey Through Genius The Great Theorems of Mathematics, 1990 (s.118)
Ya yüksekliği bilmiyorsak? Günlük hayatta karşımıza çıkan üçgenlerin kenarlarını kolayca ölçebiliriz, ama arazide yatay bir yüksekliği ölçmek hiç kolay değil.
Mesela, kenarları 17, 25 ve 28 metre olan üçgenin alanı nedir? Bu sorunun cevabı Euclid'de değil, ondan birkaç yüz sene sonra yaşamış olan Heron'un formülünde:
Alan² = (a+b+c)(b+c−a)(a+c−b)(a+b−c)/16
= (17+25+28)(25+28−17)(17+28−25)(17+25−28)/16 = 44100
Bu karmaşık görünümlü simetrik formülden Alan = 210 m² bulunur.
Formüle Giden Yol
Kolayca hatırlanacak bir formül değil... En iyisi, hazır geometri bilgimizi kullanarak, iki küçük dik üçgende yazılan iki denklemden h'yi bulmaya çalışalım:
289 − p² = 625 − 784 + 56p − p²
56p = 448 ve p = 8 bulunur.
Buradan h² = 17² − 8² = 225
h = 15 ve Alan = ch/2 = 210 sonucuna ulaştık.
Genelleme
Verilen üç uzunluk için, iki denklemle alanı hesaplamayı başardık. Peki bu hesabı a, b, c kenar uzunlukları için genelleyen Heron formülüne nasıl ulaşacağız?
h² terimlerini eşitleyince
a² − p² = b² − c² + 2cp − p²
Buradan 2cp = a² − b² + c²
ve p = (a² − b² + c²)/2c bulunur.
[Bu noktada bir nefes alıp p = a cos B olduğunu hatırlarsak, B açısı için kosinüs kuralı yan ürün olarak karşımıza çıkıyor: cos B = (a² − b² + c²)/2ac ]
Öte yandan, iki kare farkını kullanarak, bilinmeyen ifadeyi bir çarpım olarak yazabiliriz:
h² = a² − p² = (a+p)(a−p)
İki kare farkını bir daha kullanalım:
(a+p) = ((a+c)²−b²)/2c = (a+c+b)(a+c−b)/2c
Diğer çarpan da benzer şekilde şöyle hesaplanır:
(a−p) = (b²−(a−c)²)/2c = (b+a−c)(b−a+c)/2c
Bu iki ifadenin çarpımından h², onun c²/4 ile çarpımından alanın karesi bulunur:
Alan² = c²h²/4 = (a+b+c)(b+c−a)(a+c−b)(a+b−c)/16
Heron formülünün bilinen şekline ulaşmak için üçgenin yarı çevresini tanımlayalım:
2s = (a+b+c)
Bu ifadeden sıra ile 2a, 2b, 2c çıkartınca
2(s−a) = (b+c−a)
2(s−b) = (a+c−b)
2(s−c) = (a+b−c) bulunur.
Böylece Alan² = s(s−a)(s−b)(s−c) elde edilir.
Geometrik Kanıt
Bu hesap Heron zamanında yapılamazdı, çünkü cebirsel ifadeler henüz bilinmiyordu. Euclid'in yaptığı gibi, sadece uzunluklar ve oranlar kullanan geometrik bir kanıt gerekiyordu. Öncelikle açıortayların kesiştiği noktayı merkez alan iç çemberi çizelim:
α+β=28, γ+α=25, β+γ=17 denklemlerinden α=18, β=10, γ=7 bulunur.
Çemberin yarıçapı r bilinirse Alan = αr+βr+γr = sr olarak hesaplanır.
Şekilde boyalı üç merkez açının toplamının π radyan (180 derece) olduğunu not edelim, 3. ödevde gerekecek.
Heron'un karmaşık kanıtını anlamak için B'nin açıortayına çizilen dikme ile c kenarına çizilen dikmeyi H noktasında kesiştirelim ve ortaya çıkan sarı ve mavi üçgenlerde benzerlik arayalım:
Cebir kullansaydık, üç bilinmeyenli üç denklem kolayca çözülürdü. Ama cebir bilmeyince aynı işi üçgenler ve orantılarla yapmak gerekiyor!
Son iki eşitlikteki u/r oranını (18−t)/t = 28/7 şeklinde birleştirince, sadece t bilinmeyeni kalır. Paydaları paylara ekleyince orantının bozulmayacağını Heron iyi biliyordu.
Buradan 18/t = 5 ya da t = 18/5 ve ilk orantıdan r² = 10t = 36 olarak bulunur.
Daha önce bulduğumuz gibi, Alan = sr = 35x6 = 210 sonucuna ulaştık. Bu yöntemin genellemesini meraklı okuyucuya bırakıyorum.
Ödev
1. Kenar uzunlukları 15, 20, 25 cm olan üçgenin alanını her iki yöntemle hesaplayın.
2. Alanın tamsayı olduğu başka a, b, c tamsayıları bulabilir misiniz?
wikiwand.com/en/Heronian_triangle
3. Kenarları √2, 2, √10 olan üçgenin alanını formül ile hesaplayın ve temel geometri bilginizle sonucu doğrulayın.
4. Şekildeki mavi üçgenlerin benzerliğini gösterin.
5. Son hesabı genelleştirerek r² = αβγ/s ve
Alan² = sαβγ = s(s−a)(s−b)(s−c) olduğunu gösterin.
Referans
William Dunham, Journey Through Genius The Great Theorems of Mathematics, 1990 (s.118)
Altın Oran
Öyle bir sayı bulalım ki, karesi aynı sayının bir fazlası olsun:
Genellikle φ (fi) harfi ile gösterilen bu sayının tersi de bir eksiğine eşit:
Altın oran olarak bilinen φ sayısının tam ve yaklaşık değerleri:
Böylece yaklaşık olarak 1/φ ≈ 0,618, φ ≈ 1,618, φ² ≈ 2,618 bulunur.
İkinci derece x²=x+1 denkleminin iki çözümünün φ ve 1−φ olduğunu kaydedelim.
Sayısal tanımı böyle, ama bu oranın orijinal tanımı elbette yine geometrik:
"Altın oranlı dikdörtgenden bir kare kesince, küçük dörtgen ilk dörtgene benzer olsun."
Göze hoş görünen bu dikdörtgenin kenar oranına "altın oran" deniyor. İnsan yapısı bir çok sanat ve mimarlık eserinde ortaya çıktığı gibi, muhtelif canlılarda da sıkça rastlanıyor.
Düzgün beşgen ve içine çizilen yıldızda da bu oranı gözlüyoruz:
Fibonacci Sayıları
İlk değerleri F0=0 ve F1=1 olan bir dizi düşünelim.
Sonraki değerler, hep bir önceki ve iki önceki sayıların toplamı olsun:
Bu şekilde elde edilen 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... dizisine Fibonacci Sayıları deniyor. Bu sayılarla altın oranın kuvvetleri arasında ilginç iki bağıntı gizli:
Birinci bağıntıyı göstermek için, x²=x+1 denkleminin iki çözümünün φ ve 1−φ olduğunu yukarıda kaydetmiştik. Fn için şöyle bir varsayım yapılırsa
İrrasyonel φ sayısından tamsayılar üreten bu formül gerçekten şaşırtıcı.
|1−φ|<1 olduğundan, büyük n değerleri için ikinci terim ihmal edilebilir. Yaklaşık olarak
İkinci bağıntı için, φ = 1φ + 0 eşitliğinden başlayarak iki tarafı φ ile çarpalım ve sağ tarafı φ² = φ + 1 tanımını kullanarak sadeleştirelim. Bu işlemi bir kaç kere tekrarlayınca iki adet Fibonacci dizisi ile karşılaşıyoruz:
Birim kareden başlayarak, etrafına sıra ile 1, 2, 3, 5, 8, 13, 21,... boyunda kareler dizilirse, Fibonacci sarmalı (spiral) elde edilir:
Düzgün Yirmiyüzlü
Üç adet altın oranlı dikdörtgeni birbirine dik olarak yerleştirince, düzgün bir yirmiyüzlünün (icosahedron) 12 köşesi ortaya çıkar:
Ödev
1. Kenarı 1 olan düzgün beşgenin iki köşegenini çizip benzer üçgenler yardımı ile köşegen uzunluğunun φ olduğunu gösterin.
2. Şu noktaların, kenarı 2 olan eşkenar bir üçgen tanımladığını gösterin:
(0, 1, φ) (1, φ, 0) (φ, 0, 1)
3. φn = Fnφ + Fn−1 bağıntısını tümevarımla gösterin.
Referans
https://www.goldennumber.net/what-is-phi/
https://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html
https://www.wikiwand.com/en/Fibonacci_number
φ² = φ + 1
Genellikle φ (fi) harfi ile gösterilen bu sayının tersi de bir eksiğine eşit:
1/φ = φ − 1
Altın oran olarak bilinen φ sayısının tam ve yaklaşık değerleri:
φ = (1+√5)/2 ≈ 1,6180
Böylece yaklaşık olarak 1/φ ≈ 0,618, φ ≈ 1,618, φ² ≈ 2,618 bulunur.
İkinci derece x²=x+1 denkleminin iki çözümünün φ ve 1−φ olduğunu kaydedelim.
Sayısal tanımı böyle, ama bu oranın orijinal tanımı elbette yine geometrik:
"Altın oranlı dikdörtgenden bir kare kesince, küçük dörtgen ilk dörtgene benzer olsun."
Göze hoş görünen bu dikdörtgenin kenar oranına "altın oran" deniyor. İnsan yapısı bir çok sanat ve mimarlık eserinde ortaya çıktığı gibi, muhtelif canlılarda da sıkça rastlanıyor.
Düzgün beşgen ve içine çizilen yıldızda da bu oranı gözlüyoruz:
Fibonacci Sayıları
İlk değerleri F0=0 ve F1=1 olan bir dizi düşünelim.
Sonraki değerler, hep bir önceki ve iki önceki sayıların toplamı olsun:
Fn+1 = Fn + Fn−1 n=1,2,3,...
Bu şekilde elde edilen 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... dizisine Fibonacci Sayıları deniyor. Bu sayılarla altın oranın kuvvetleri arasında ilginç iki bağıntı gizli:
Fn = (φn−(1−φ)n)/√5 ve
φn = Fnφ + Fn−1 n=1,2,3,...
φn = Fnφ + Fn−1 n=1,2,3,...
Birinci bağıntıyı göstermek için, x²=x+1 denkleminin iki çözümünün φ ve 1−φ olduğunu yukarıda kaydetmiştik. Fn için şöyle bir varsayım yapılırsa
Fn = Aφn + B(1−φ)n
F0=0 ve F1=1 eşitliklerinden A = −B = 1/√5 bulunur.İrrasyonel φ sayısından tamsayılar üreten bu formül gerçekten şaşırtıcı.
|1−φ|<1 olduğundan, büyük n değerleri için ikinci terim ihmal edilebilir. Yaklaşık olarak
Fn ≈ φn/√5 ve
Fn+1/Fn ≈ φ
Fn+1/Fn ≈ φ
İkinci bağıntı için, φ = 1φ + 0 eşitliğinden başlayarak iki tarafı φ ile çarpalım ve sağ tarafı φ² = φ + 1 tanımını kullanarak sadeleştirelim. Bu işlemi bir kaç kere tekrarlayınca iki adet Fibonacci dizisi ile karşılaşıyoruz:
φ1 = 1φ + 0
φ2 = 1φ + 1
φ3 = 2φ + 1
φ4 = 3φ + 2
φ5 = 5φ + 3
φ6 = 8φ + 5
Birim kareden başlayarak, etrafına sıra ile 1, 2, 3, 5, 8, 13, 21,... boyunda kareler dizilirse, Fibonacci sarmalı (spiral) elde edilir:
Düzgün Yirmiyüzlü
Üç adet altın oranlı dikdörtgeni birbirine dik olarak yerleştirince, düzgün bir yirmiyüzlünün (icosahedron) 12 köşesi ortaya çıkar:
Ödev
1. Kenarı 1 olan düzgün beşgenin iki köşegenini çizip benzer üçgenler yardımı ile köşegen uzunluğunun φ olduğunu gösterin.
2. Şu noktaların, kenarı 2 olan eşkenar bir üçgen tanımladığını gösterin:
(0, 1, φ) (1, φ, 0) (φ, 0, 1)
3. φn = Fnφ + Fn−1 bağıntısını tümevarımla gösterin.
Referans
https://www.goldennumber.net/what-is-phi/
https://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html
https://www.wikiwand.com/en/Fibonacci_number
Euler Formülü
1700'lü yıllarda yaşamış Euler'in adıyla anılan en az dört formül var matematik dünyasında. "Euler formula" şeklinde arayınca bunları ve daha fazlasını bulmak mümkün:
Yukarıdaki ilk formülde, üstel fonksiyonun değerini sanal bir argümanla hesaplayınca beklenmedik bir şekilde, trigonometrik fonksiyonlar karşımıza çıkıyor. Bunun x=π için özel hali, 0, 1, e, π ve i sayılarını ikinci formülde bir araya getiriyor. Üçüncü formül, Euler sayısını bir limit olarak hesaplıyor.
En alttaki formül, topolojinin en ilginç kuralını özetliyor: V+F = E+2
Kural, köşeleri birbirine bağlı bir harita (matematik dilinde connected map) için tanımlanan V, E, F kümelerinin eleman sayıları arasındaki değişmez bir bağıntıyı ifade ediyor.
V = köşeler (vertices) kümesi ya da sayısı
E = kenarlar (edges) kümesi ya da sayısı
F = bölgeler (faces) kümesi ya da sayısı
Cebirde bir sembole ancak bir anlam yüklenir. Burada bir kargaşa söz konusu olmadığı için, V, E, F sembolleri yerine göre kümeleri ya da eleman sayılarını gösteriyor olabilir.
Örnek: Şekildeki map M = (V, E, F) üçlüsü ile gösterilir.
V = {a, b, d, e, f} köşelerini 7 kenarla birleştirince
E = {ab, ad, bb, bf, bf, de, df} ve F = {A, B, C, D} elde edilir.
Normal bir kümede elemanların tekrarına izin yoktur. Lakin burada b'den f'ye iki kenar olduğundan, E içindeki elemanlar birden fazla olabiliyor. Multiset denen bu kavram, map konusunu çalışırken karşımıza çıkan ilk ayrıcalık. Bir diğeri de, düzlem geometride mümkün olmayan birgen ve ikigenler!
Bu örnekte B bölgesi birgen, D bölgesi ise ikigen. Şeklin dışındaki C bölgesinin sınırları abbfd olduğundan bir beşgen tanımlıyor. A bölgesi ise abfded şeklinde bir altıgen. Bu çokgenlerin kenar sayılarını toplayınca 6+1+5+2 = 14 bulunur ki, map içindeki kenar sayısının iki katıdır. Neden? Çünkü her kenarı iki kere saydık.
Benzer şekilde, her köşedeki kenar sayılarını toplayınca aynı 2+5+3+1+3 = 14 değeri bulunur. Bu iki denklemi genelleştirince, Euler formülüne ek olarak şu ifadeler bulunur:
Kanıt
Euler formülünün doğruluğuna ikna olmak için boş bir map ile başlayalım ve kenarları birer birer ekleyerek istenen M'ye ulaşalım. Boş map M0 içinde hiç kenar olmasın, sadece bir köşe ile başlayalım.
Birinci adımda köşeleri ekleyelim. Her köşe için bir kenar gerektiğine göre, M1 şekline ulaşınca V−1 kenar eklenmiş oldu.
İkinci adımda hazır köşeleri birleştirerek bölgeleri ekleyelim. Her bölge için bir kenar gerektiğine göre, M şekline ulaşınca F−1 kenar daha eklenmiş oldu. Toplam (V−1)+(F−1) kenar eklediğimize göre aranan E = V+F−2 eşitliğine ulaştık.
Kanıt burada tamamlandı ama V+F = E+2 bağıntısının değişmezliğini de kullanabilirdik. M0 için V=1, E=0, F=1 olduğundan verilen denklem başlangıçta doğru. Her kenarı eklerken ya bir köşe ya da bir bölge eklendiğinden denklem değişmez, M için de doğrudur.
Dual Map
Köşelerle bölgelerin yerini değiştirince dual map ortaya çıkar:
Bu örneğin dualinde V' = {A, B, C, D} ve F' = {a, b, d, e, f} olur.
Kenarlar ise, birleştirdiği iki köşe yerine ayırdığı iki bölge ile anılır:
E = {ab, ad, bb, bf, bf, de, df} yerine
E' = {AC, AC, BC, AD, CD, AA, AC}
Dual map için farklı çizimler olabilir. Ancak, dualin duali yine orijinal map olacaktır.
Düzgün (Regular) Map
Öyle bir map düşünelim ki, her bölgesi p-gen olsun ve her köşesinde q kenar buluşsun. Euler formülünün sonucu olarak, p ve q sayıları keyfi seçilemez,
pF = 2E , qV = 2E ve V+F = E+2 kısıtlarını sağlamak zorundayız.
p=2 halinde, V=2 ve F=E=q bulunur, q kenarla dış bölge dahil q adet ikigen çizilebilir.
q=2 halinde, F=2 ve V=E=p bulunur, p kenarla dış bölge dahil 2 adet p-gen çizilebilir.
Çok ilginç olmayan bu özel halleri göz ardı edip p>2 ve q>2 varsayarsak, (p-2)(q-2)<4 kısıtı bulunur ki, p ve q sayıları için sadece aşağıda gösterilen beş çözüm bulunur. Sonraki konumuzda işlenen düzgün çokyüzlülerin düzlemdeki modellerini bulmuş olduk.
Ödev
1. Dört bölgesinin kenar sayıları {1, 2, 3, 4} olan mapi ve duallerinden birini çizin.
(ipucu: Neden E=5? O halde V kaç olmalı?)
2. Şekilde gösterilen beş adet düzgün map için p ve q değerlerini bulun.
Referans
http://mathworld.wolfram.com/EulerFormula.html
https://www.wikiwand.com/en/List_of_things_named_after_Leonhard_Euler
Yukarıdaki ilk formülde, üstel fonksiyonun değerini sanal bir argümanla hesaplayınca beklenmedik bir şekilde, trigonometrik fonksiyonlar karşımıza çıkıyor. Bunun x=π için özel hali, 0, 1, e, π ve i sayılarını ikinci formülde bir araya getiriyor. Üçüncü formül, Euler sayısını bir limit olarak hesaplıyor.
En alttaki formül, topolojinin en ilginç kuralını özetliyor: V+F = E+2
Kural, köşeleri birbirine bağlı bir harita (matematik dilinde connected map) için tanımlanan V, E, F kümelerinin eleman sayıları arasındaki değişmez bir bağıntıyı ifade ediyor.
V = köşeler (vertices) kümesi ya da sayısı
E = kenarlar (edges) kümesi ya da sayısı
F = bölgeler (faces) kümesi ya da sayısı
Cebirde bir sembole ancak bir anlam yüklenir. Burada bir kargaşa söz konusu olmadığı için, V, E, F sembolleri yerine göre kümeleri ya da eleman sayılarını gösteriyor olabilir.
Örnek: Şekildeki map M = (V, E, F) üçlüsü ile gösterilir.
V = {a, b, d, e, f} köşelerini 7 kenarla birleştirince
E = {ab, ad, bb, bf, bf, de, df} ve F = {A, B, C, D} elde edilir.
Normal bir kümede elemanların tekrarına izin yoktur. Lakin burada b'den f'ye iki kenar olduğundan, E içindeki elemanlar birden fazla olabiliyor. Multiset denen bu kavram, map konusunu çalışırken karşımıza çıkan ilk ayrıcalık. Bir diğeri de, düzlem geometride mümkün olmayan birgen ve ikigenler!
Bu örnekte B bölgesi birgen, D bölgesi ise ikigen. Şeklin dışındaki C bölgesinin sınırları abbfd olduğundan bir beşgen tanımlıyor. A bölgesi ise abfded şeklinde bir altıgen. Bu çokgenlerin kenar sayılarını toplayınca 6+1+5+2 = 14 bulunur ki, map içindeki kenar sayısının iki katıdır. Neden? Çünkü her kenarı iki kere saydık.
Benzer şekilde, her köşedeki kenar sayılarını toplayınca aynı 2+5+3+1+3 = 14 değeri bulunur. Bu iki denklemi genelleştirince, Euler formülüne ek olarak şu ifadeler bulunur:
Kanıt
Euler formülünün doğruluğuna ikna olmak için boş bir map ile başlayalım ve kenarları birer birer ekleyerek istenen M'ye ulaşalım. Boş map M0 içinde hiç kenar olmasın, sadece bir köşe ile başlayalım.
İkinci adımda hazır köşeleri birleştirerek bölgeleri ekleyelim. Her bölge için bir kenar gerektiğine göre, M şekline ulaşınca F−1 kenar daha eklenmiş oldu. Toplam (V−1)+(F−1) kenar eklediğimize göre aranan E = V+F−2 eşitliğine ulaştık.
Kanıt burada tamamlandı ama V+F = E+2 bağıntısının değişmezliğini de kullanabilirdik. M0 için V=1, E=0, F=1 olduğundan verilen denklem başlangıçta doğru. Her kenarı eklerken ya bir köşe ya da bir bölge eklendiğinden denklem değişmez, M için de doğrudur.
Dual Map
Köşelerle bölgelerin yerini değiştirince dual map ortaya çıkar:
Bu örneğin dualinde V' = {A, B, C, D} ve F' = {a, b, d, e, f} olur.
Kenarlar ise, birleştirdiği iki köşe yerine ayırdığı iki bölge ile anılır:
E = {ab, ad, bb, bf, bf, de, df} yerine
E' = {AC, AC, BC, AD, CD, AA, AC}
Düzgün (Regular) Map
Öyle bir map düşünelim ki, her bölgesi p-gen olsun ve her köşesinde q kenar buluşsun. Euler formülünün sonucu olarak, p ve q sayıları keyfi seçilemez,
pF = 2E , qV = 2E ve V+F = E+2 kısıtlarını sağlamak zorundayız.
p=2 halinde, V=2 ve F=E=q bulunur, q kenarla dış bölge dahil q adet ikigen çizilebilir.
q=2 halinde, F=2 ve V=E=p bulunur, p kenarla dış bölge dahil 2 adet p-gen çizilebilir.
Çok ilginç olmayan bu özel halleri göz ardı edip p>2 ve q>2 varsayarsak, (p-2)(q-2)<4 kısıtı bulunur ki, p ve q sayıları için sadece aşağıda gösterilen beş çözüm bulunur. Sonraki konumuzda işlenen düzgün çokyüzlülerin düzlemdeki modellerini bulmuş olduk.
Ödev
1. Dört bölgesinin kenar sayıları {1, 2, 3, 4} olan mapi ve duallerinden birini çizin.
(ipucu: Neden E=5? O halde V kaç olmalı?)
2. Şekilde gösterilen beş adet düzgün map için p ve q değerlerini bulun.
Referans
http://mathworld.wolfram.com/EulerFormula.html
https://www.wikiwand.com/en/List_of_things_named_after_Leonhard_Euler
Çokyüzlüler
Düzgün çokyüzlüler matematikçileri asırlarca büyülemiş.

Ödev
1. Fig 8.38 is made by dividing the faces of an icosahedron to triangles.
Determine V, F, E
2. Consider eight points on the plane: (±1,±a) (±a,±1)
Determine a so that they are the vertices of a regular octagon
3. Show that the points (0,1,2) ... (2,1,0) form a regular hexagon
(Use all permutations of 0, 1, and 2)
4. Consider the 20 vertices of the dodecahedron: (±1,±1,±1) (±a,±ϕ,0) (±ϕ,0,±a) (0,±a,±ϕ)
where ϕ = 1/a is the golden mean with a² = 1-a
Show that the vertices on the plane x+ay=ϕ form a regular pentagon with side 2a
Referans

Ödev
1. Fig 8.38 is made by dividing the faces of an icosahedron to triangles.
Determine V, F, E
2. Consider eight points on the plane: (±1,±a) (±a,±1)
Determine a so that they are the vertices of a regular octagon
3. Show that the points (0,1,2) ... (2,1,0) form a regular hexagon
(Use all permutations of 0, 1, and 2)
4. Consider the 20 vertices of the dodecahedron: (±1,±1,±1) (±a,±ϕ,0) (±ϕ,0,±a) (0,±a,±ϕ)
where ϕ = 1/a is the golden mean with a² = 1-a
Show that the vertices on the plane x+ay=ϕ form a regular pentagon with side 2a
Referans
Kübik Simetri
Kübün bir yüzüne yukardan bakınca 4'lü simetriyi görebiliriz

Ödev
* Starting pages: Fig 7.28 and Sec 9.9
https://en.wikipedia.org/wiki/Archimedean_solid
* First three pictures show how to make 9 circles of Oh symmetry
and 48 triangles in the dual solid of 4.6.8
* Escher's drawing (Ref 5) may help you visualise:
http://math.slu.edu/escher/upload/4/44/Concentric-rinds.jpg
Referans

Ödev
* Starting pages: Fig 7.28 and Sec 9.9
https://en.wikipedia.org/wiki/Archimedean_solid
* First three pictures show how to make 9 circles of Oh symmetry
and 48 triangles in the dual solid of 4.6.8
* Escher's drawing (Ref 5) may help you visualise:
http://math.slu.edu/escher/upload/4/44/Concentric-rinds.jpg
Referans
Çokyüzlü Dönüşümleri
Truncate: Vertices are truncated until each face becomes a regular polygon. If
the original solid has v vertices and e edges, the truncated solid will have 2e vertices
and 3e edges. In symbols, (v,e) -> (2e,3e) with q= 3. [q is the number edges at each vertex]
Rectify: The midpoints of each edge are connected so that each original face and
vertex becomes a face. If the original solid has v vertices and e edges, the rectified
solid will have e vertices and 2e edges. In symbols, (v,e) -> (e,2e) with q= 4.
Snub: Each vertex becomes a triangle, faces are rotated slightly until each edge
becomes two triangles. In symbols, (v,e) -> (2v,5v) with q = 5.

Ödev
* First three pictures show how to make 9 circles of Oh symmetry
and 48 triangles in the dual solid of 4.6.8
* Escher's drawing (Ref 5) may help you visualise:
http://math.slu.edu/escher/upload/4/44/Concentric-rinds.jpg
* Fourth picture shows the other Catalan solids with Oh symmetry
http://en.wikipedia.org/wiki/Catalan_solid
* Show the effect of these transformations on the last picture
Truncate: (v,e,f) -> (2e,3e,e+2)
Rectify: (v,e,f) -> (e,2e,e+2)
Snub: (v,e,f) -> (e,5e/2,3e/2+2)
Referans
the original solid has v vertices and e edges, the truncated solid will have 2e vertices
and 3e edges. In symbols, (v,e) -> (2e,3e) with q= 3. [q is the number edges at each vertex]
Rectify: The midpoints of each edge are connected so that each original face and
vertex becomes a face. If the original solid has v vertices and e edges, the rectified
solid will have e vertices and 2e edges. In symbols, (v,e) -> (e,2e) with q= 4.
Snub: Each vertex becomes a triangle, faces are rotated slightly until each edge
becomes two triangles. In symbols, (v,e) -> (2v,5v) with q = 5.

Ödev
* First three pictures show how to make 9 circles of Oh symmetry
and 48 triangles in the dual solid of 4.6.8
* Escher's drawing (Ref 5) may help you visualise:
http://math.slu.edu/escher/upload/4/44/Concentric-rinds.jpg
* Fourth picture shows the other Catalan solids with Oh symmetry
http://en.wikipedia.org/wiki/Catalan_solid
* Show the effect of these transformations on the last picture
Truncate: (v,e,f) -> (2e,3e,e+2)
Rectify: (v,e,f) -> (e,2e,e+2)
Snub: (v,e,f) -> (e,5e/2,3e/2+2)
Referans
Tamsayılarla 4 İşlem
Üç elma ile üç kalemi yan yana koyup bire bir eşlemeyi görmek, buradan "üç" sayısına ulaşmak önemli bir soyutlama... Hele şu "yedi"lerin ortak özelliğini anlamak, konuşmayı yeni öğrenen bir buçuk yaşındaki Ruya Ada için kolay mı?
Toplama
Bir tabaktaki üç hurma ile başka bir tabaktaki iki hurmayı birleştirince, toplam beş hurmamız olduğunu 3+2=5 şeklinde sembollerle ifade ediyoruz. Bu ifadenin gücü, toplanan şeylerden bağımsız olması... Yani elmalar, saatler, liralar, vb aynı şekilde toplanabilir.
Toplama işleminin özelliklerini cebirsel ifadelerle anlayalım. Rastgele seçilen üç doğal sayı a, b, c olsun. Aşağıdaki özelliklerin, kümelerin davranışından kaynaklandığı kolayca görülebilir:
Çarpma
Sıradaki ikinci işlem çıkarma değil çarpma: Bir a sayısından hiç almazsak sonuç sıfır, bir tane alırsak a, iki tane alırsak a+a, ... Bu diziyi nasıl genelleyelim?
0a = 0
1a = 0a+a
2a = 1a+a
3a = 2a+a
...
(b+1)a = ba+a
İlk ve son formül, her a ve b doğal sayısının çarpımını tanımlıyor. Bu tanımdan yola çıkarak çarpmanın özelliklerine ulaşabiliriz:
Çıkarma
Çıkarma işleminin zorluğu, doğal sayılarda kapalı olmaması. Mesela üçten beş çıkmayacağını küçük yaşta öğrenmiştik. Sorun, sıfırdan önceki sayının yokluğu... Bir sayıdan, kendisinden daha büyük bir sayı çıkarabilmek için negatif sayılar gerekiyor. Bu anlayışa ancak ortaokul yaşlarına ulaştık.
Negatif sayıları tanımlamak amacı ile 1−1=0 eşitliğini −1+1=0 şeklinde yazmak, sıfırdan sonraki en önemli keşfimiz olabilir: Böyle yazınca, "eksi bir" de "bir" gibi sayı oldu! Bu sayı, "bir"in negatifi, çünkü bir ekleyince sıfır çıkıyor. İşte, sıfırdan önceki doğal olmayan sayı bu...
Şimdi bu son eşitliği bir a doğal sayısı ile çarpalım: (−1)a+a = 0
(−1)a sayısını −a şeklinde gösterirsek, her sayının negatifini elde ederiz: −a+a = 0
Artık çıkarma işlemi şöyle tanımlanabilir: b−a = b+(−a)
Böylece, "çıkarma, toplamanın ters işlemi" denilebilir: (b−a)+a = b+(−a)+a = b
Bu tanımın geçerli olması için, her sayının negatifini doğal sayılar kümesine ekliyor ve tamsayılar kümesine ulaşıyoruz. Toplama ve çarpmanın yukarıda sayılan bütün özellikleri negatif tamsayılar de geçerli. Lakin, çıkarma işleminde bu özelliklerin çoğu kayboluyor:
−2+2 = 0 eşitliğini mesela (−3) ile çarpalım
(−2)(−3)+2(−3) = 0(−3)
(−2)(−3)+(−6) = 0
Demek ki (−2)(−3) = 6 olmalı, çünkü −6 ekleyince sıfır çıkıyor.
Bölme
Tamsayılar dünyasında çarpmanın tersi çok kısıtlı bir işlem. Mesela 20 sayısının bölenlerini bulalım:
20 = 1×20 = 2×10 = 4×5 olduğuna göre, 20'nin bölenleri {1, 2, 4, 5, 10, 20} kümesinden ibaret. Yani 20 sayısı ancak bu sayıların biriyle bölünebilir.
Böylece, bölme de çarpmanın ters işlemi oldu: (b/a)a = b
Sıfır ise hiçbir sayının böleni olmadığına göre hiçbir sayı asla sıfıra bölünemez. Sıfıra bölmek matematikte ve yazılımda önemli bir hata kabul edilir.
Bu kadar kısıtlı bir işlemin fazla özelliği olmayacağı açık:
Ödev
1. Sıfır özelliğini taşıyan her sayının sıfıra eşit olması gerektiğini gösterin:
Her a için s+a = a ise, s=0 olmalı
2. Bölmenin dağılma özelliğini a=5, b=75, c=25 sayıları ile doğrulayın
Not: Bu yazıyı sevgili kuzenim Halid Abay'a ithaf ediyorum 11 Mayıs 2018
- Gökkuşağında yedi renk var
- Piyanoda yedi notayı dinle
- Yedinci katta oturuyoruz
- Baban yedide gelecek
- Prenses ve yedi cüce
Toplama
Bir tabaktaki üç hurma ile başka bir tabaktaki iki hurmayı birleştirince, toplam beş hurmamız olduğunu 3+2=5 şeklinde sembollerle ifade ediyoruz. Bu ifadenin gücü, toplanan şeylerden bağımsız olması... Yani elmalar, saatler, liralar, vb aynı şekilde toplanabilir.
Toplama işleminin özelliklerini cebirsel ifadelerle anlayalım. Rastgele seçilen üç doğal sayı a, b, c olsun. Aşağıdaki özelliklerin, kümelerin davranışından kaynaklandığı kolayca görülebilir:
- Değişme: a+b = b+a Toplamayı hangi sırada yaptığımızın önemi yok
- Birleşme: (a+b)+c = a+(b+c) Önce hangi toplamayı yaptığımızın önemi yok
- Sıfır: 0+a = a Bir sayıya sıfır ekleyince sayı değişmez
Çarpma
Sıradaki ikinci işlem çıkarma değil çarpma: Bir a sayısından hiç almazsak sonuç sıfır, bir tane alırsak a, iki tane alırsak a+a, ... Bu diziyi nasıl genelleyelim?
0a = 0
1a = 0a+a
2a = 1a+a
3a = 2a+a
...
(b+1)a = ba+a
İlk ve son formül, her a ve b doğal sayısının çarpımını tanımlıyor. Bu tanımdan yola çıkarak çarpmanın özelliklerine ulaşabiliriz:
- Değişme: ab = ba Çarpmayı hangi sırada yaptığımızın önemi yok
- Birleşme: (ab)c = a(bc) Önce hangi çarpmayı yaptığımızın önemi yok
- Sıfır: 0a = 0 Bir sayıyı sıfırla çarpınca sıfır çıkar
- Bir: 1a = a Bir sayıyı birle çarpınca sayı değişmez
- Dağılma: (b+c)a = ba+ca Ortak çarpanla bir kere çarpmak yeterli
Çıkarma
Çıkarma işleminin zorluğu, doğal sayılarda kapalı olmaması. Mesela üçten beş çıkmayacağını küçük yaşta öğrenmiştik. Sorun, sıfırdan önceki sayının yokluğu... Bir sayıdan, kendisinden daha büyük bir sayı çıkarabilmek için negatif sayılar gerekiyor. Bu anlayışa ancak ortaokul yaşlarına ulaştık.
Negatif sayıları tanımlamak amacı ile 1−1=0 eşitliğini −1+1=0 şeklinde yazmak, sıfırdan sonraki en önemli keşfimiz olabilir: Böyle yazınca, "eksi bir" de "bir" gibi sayı oldu! Bu sayı, "bir"in negatifi, çünkü bir ekleyince sıfır çıkıyor. İşte, sıfırdan önceki doğal olmayan sayı bu...
Şimdi bu son eşitliği bir a doğal sayısı ile çarpalım: (−1)a+a = 0
(−1)a sayısını −a şeklinde gösterirsek, her sayının negatifini elde ederiz: −a+a = 0
Artık çıkarma işlemi şöyle tanımlanabilir: b−a = b+(−a)
Böylece, "çıkarma, toplamanın ters işlemi" denilebilir: (b−a)+a = b+(−a)+a = b
Bu tanımın geçerli olması için, her sayının negatifini doğal sayılar kümesine ekliyor ve tamsayılar kümesine ulaşıyoruz. Toplama ve çarpmanın yukarıda sayılan bütün özellikleri negatif tamsayılar de geçerli. Lakin, çıkarma işleminde bu özelliklerin çoğu kayboluyor:
- Değişme yok: a−b = −(b−a) Sıra değişince işaret de değişir
- Birleşme yok: (a−b)−c = a−(b+c), a−(b−c) = (a−b)+c
- Sıfır: a−0 = a, 0−a = −a
- Dağılma var: (b−c)a = ba−ca
−2+2 = 0 eşitliğini mesela (−3) ile çarpalım
(−2)(−3)+2(−3) = 0(−3)
(−2)(−3)+(−6) = 0
Demek ki (−2)(−3) = 6 olmalı, çünkü −6 ekleyince sıfır çıkıyor.
Bölme
Tamsayılar dünyasında çarpmanın tersi çok kısıtlı bir işlem. Mesela 20 sayısının bölenlerini bulalım:
20 = 1×20 = 2×10 = 4×5 olduğuna göre, 20'nin bölenleri {1, 2, 4, 5, 10, 20} kümesinden ibaret. Yani 20 sayısı ancak bu sayıların biriyle bölünebilir.
Böylece, bölme de çarpmanın ters işlemi oldu: (b/a)a = b
Sıfır ise hiçbir sayının böleni olmadığına göre hiçbir sayı asla sıfıra bölünemez. Sıfıra bölmek matematikte ve yazılımda önemli bir hata kabul edilir.
Bu kadar kısıtlı bir işlemin fazla özelliği olmayacağı açık:
- Değişme yok: a=±b değilse a/b ≠ b/a
- Birleşme yok: c=±1 değilse (a/b)/c ≠ a/(b/c)
- Sıfır: 0/a = 0 Sıfırı bir sayıya bölünce sıfır çıkar (a≠0)
(a/0 tanımsızdır, sıfıra bölmek önemli bir hatadır) - Bir: a/1 = a Bir sayıyı bire bölünce sayı değişmez
- Dağılma var: (b±c)/a = (b/a)±(c/a)
Ödev
1. Sıfır özelliğini taşıyan her sayının sıfıra eşit olması gerektiğini gösterin:
Her a için s+a = a ise, s=0 olmalı
2. Bölmenin dağılma özelliğini a=5, b=75, c=25 sayıları ile doğrulayın
Not: Bu yazıyı sevgili kuzenim Halid Abay'a ithaf ediyorum 11 Mayıs 2018
Sayı Türleri
Asırlar boyunca "sayı" kavramı çok gelişti. Bu bölümde N, Z, Q, R, C kümeleri ile adlandırılan beş çeşit sayıyı incelerken, doğal sayılarla başlayıp kompleks sayılarla biten bir yolculuk yapalım.
Euclid ve çağdaşları için, sayı -adı üstünde- sayılabilen sayılardan ibaret idi: Doğal sayılar olarak isim verdiğimiz N kümesi. Son bin seneye kadar sıfır sayı olarak bile görülmüyordu ama bugünkü anlayışımıza göre 0 bu kümenin en önemli üyesi.
İki doğal sayı a ve b verildiğinde, bunlar arasında bir sıralama söz konusu:
a<b veya a=b ya da a>b durumlarından sadece biri doğru olmak zorunda. Sayılar büyük olduğunda sıralamak için biraz uğraşmak gerekebilir. Mesela şu sayıların hangisi daha büyük: 123456789 ve 1234112233?
Ya da şu iki kümenin eleman sayısının aynı olduğunu görüyor musunuz?
A = { a | a²=9 } B = { 4, 2+3, 6-2, 5 }
Doğal sayılarla toplama ve çarpma yapmayı küçük yaşlarda öğrendiğimiz için bu iki işlemi hiç yadırgamayız. Ne kadar büyük olursa olsun, bana iki sayı verin, toplamını ve çarpımını hemen bulabilirim. Sıfır ve bir sayılarının özel önemini, her a doğal sayısı için doğru olan şu eşitlikler belirliyor:
0+a = a 0a = 0 1a = a
Toplama ve çarpmanın temel özelliklerini kaydedelim. Verilen a, b, c doğal sayıları için:
a+b = b+a a+(b+c) = (a+b)+c = a+b+c
ab = ba a(bc) = (ab)c =abc (a+b)c = ac+ab
Toplamadan çarpmaya şu kuralla geçilebilir: ab = a(b-1)+a (b>0 ise)
Yani 2a=a+a ve 3a=2a+a
Aynı şekilde, üs alma işlemi çarpma üstünden tanımlanabilir: ab = ab-1a (b>0 ise)
Yani a²=aa ve a³=a²a
Toplama için artı işareti kullanıldığı halde, standart cebirde çarpma için bir sembol çoğu zaman gerekmez. 12a ifadesi a'nın 12 katını gösterir. Ancak iki sabit sayıyı çarpmak gerektiğinde araya nokta (⋅) ya da çarpı (×) koymak gerekir: 12×5 gibi...
Çıkarma işlemini toplamanın tersi olarak tanımlayalım: 7−4=3 çünkü 7=3+4
Ama 4−7 işlemine gelince, "4'ten 7 çıkmaz" diyoruz çünkü 4<7.
Benzer bir şekilde, 2×5=10 olduğundan, 10/5=2 ama "10 sayısı 3'e bölünmez" diyoruz doğal sayılar kümesinde.
Negatif Sayılar
Doğal sayılara yapacağımız ilk ekleme çıkarma işlemini genelleştirmemizi sağlıyor. Öyle bir m sayısı "icat edelim" ki 1+m=0 olsun. Bu m sayısı doğal değil, çünkü m hiçbir kümenin eleman sayısı olamaz. Peki m sayısı ne işe yarar?
Her doğal sayıdan önceki sayıyı ve sonraki sayıyı kolayca bulabiliriz -- sıfır hariç. "Sıfırdan önceki sayı m olsun" varsayımı ile m'yi ve m'nin katlarını N kümesine eklersek Z (tamsayılar) kümesine ulaşırız.
Tanım denklemini 2 ile çarpınca (1+m)2=2+m2=0 buluyoruz. O halde m2 (m'nin 2 katı) sayısı 2'nin toplamaya göre tersi, yani negatifi olur. Bunu −2 olarak gösterince negatif sayıları tanımlamış olduk.
Tanım denklemini m ile çarpınca (1+m)m=m+m²=0 buluyoruz. Bu denklemin iki tarafına 1 ekleyince 1+m+m²=1 ya da m²=1 özelliğini cebirsel işlemlerle kanıtlarız.
Yukarıda söz konusu olan 4−7 işlemini 4+m7 olarak tanımlayıp m7=m(4+3)=m4+m3 özelliğini kullanarak 4−7=4+m4+m3=m3 yani −3 sonucunu buluruz.
Kesirli Sayılar
Her kesir için 2/3=10/15=30/45 gibi sınırsız sayıda gösterim var.
Doğal sayılar için de durum aynı: 7/1=35/5=105/15
0/b şeklindeki kesirler, doğal sıfırın özelliklerini taşıdığı için 0 olarak yazılır.
b/b şeklindeki kesirler, doğal birin özelliklerini taşıdığı için 1 olarak yazılır.
Verilen bir p sayısının negatifi, tamsayılarda olduğu gibi −p ile gösterilir ve p+(−p)=0 özdeşliğini sağlar. Negatifi kendisine eşit olan tek sayı sıfırdır. Verilen bir p sayısının tersi, p-1 ile gösterilir ve p(p-1)=1 özdeşliğini sağlar. p=a/b sayısının tersi, a=0 durumunda tanımsızdır. Sıfır değilse, tanım gereği mesela 8'in tersi 1/8, −3/5'in tersi −5/3 olarak bulunur. Tersi kendisine eşit olan tek sayı birdir.
Kesirli sayıları da ekleyince Q (rasyonel sayılar) kümesine ulaşmış olduk. Rasyonel sayılar kümesinde dört işlemi eksiksiz tanımlamış olduk. Bilgisayarların kullandığı aritmetik de rasyonel olduğuna göre, bütün sayısal uygulamalar bu kümenin içindedir denilebilir.
İrrasyonel Sayılar
Uygulamayı etkilemeyen, ama matematikçileri rahatsız eden önemli bir sorun kaldı: Kenarları birim uzunluktaki eşkenar üçgenin yüksekliğini ya da karenin köşegenini rasyonel sayı olarak yazamazsınız. Başka bir deyişle, 2'nin ya da 3'ün kare kökü iki tamsayının oranı değildir!
Üstelik bu sorun kare köklerle sınırlı değil. Bütün rasyonel sayıların bütün köklerini eklesek bile, aralarında sonsuz irrasyonel sayı kalıyor.
Sanal Sayılar
Yolculuğumuzun son durağında bir sayı türü daha gerekecek. Negatif sayıları göstermek için 1+m=0 şartını sağlayan bir tek sayı icat etmek yeterli olmuştu. Sanal sayılara geçmek için de i²=m şartını sağlayan bir i sayısı gerekiyor -- gerisi düz cebir:
Sonuç
Ödev
1. z=5+12i sayısının iki kare kökünü
a) (x+iy)²=z eşitliğinden iki denklem yazarak,
b) polar koordinatlar kullanarak bulun
2. Bir'in dördüncü köklerini bulun
(z⁴=1 denkleminin 4 farklı kökü var)
3. Google and Wolfram'a "log(-1)" sorunca farklı cevaplar geliyor:
www.wolframalpha.com/input/?i=log+(-1)
www.google.com/search?q=log(-1)
Hangisi doğrusu?
Referans
https://www.wikiwand.com/en/Number
http://www.feynmanlectures.caltech.edu/I_22.html
Euclid ve çağdaşları için, sayı -adı üstünde- sayılabilen sayılardan ibaret idi: Doğal sayılar olarak isim verdiğimiz N kümesi. Son bin seneye kadar sıfır sayı olarak bile görülmüyordu ama bugünkü anlayışımıza göre 0 bu kümenin en önemli üyesi.
İki doğal sayı a ve b verildiğinde, bunlar arasında bir sıralama söz konusu:
a<b veya a=b ya da a>b durumlarından sadece biri doğru olmak zorunda. Sayılar büyük olduğunda sıralamak için biraz uğraşmak gerekebilir. Mesela şu sayıların hangisi daha büyük: 123456789 ve 1234112233?
Ya da şu iki kümenin eleman sayısının aynı olduğunu görüyor musunuz?
A = { a | a²=9 } B = { 4, 2+3, 6-2, 5 }
Doğal sayılarla toplama ve çarpma yapmayı küçük yaşlarda öğrendiğimiz için bu iki işlemi hiç yadırgamayız. Ne kadar büyük olursa olsun, bana iki sayı verin, toplamını ve çarpımını hemen bulabilirim. Sıfır ve bir sayılarının özel önemini, her a doğal sayısı için doğru olan şu eşitlikler belirliyor:
0+a = a 0a = 0 1a = a
Toplama ve çarpmanın temel özelliklerini kaydedelim. Verilen a, b, c doğal sayıları için:
a+b = b+a a+(b+c) = (a+b)+c = a+b+c
ab = ba a(bc) = (ab)c =abc (a+b)c = ac+ab
Toplamadan çarpmaya şu kuralla geçilebilir: ab = a(b-1)+a (b>0 ise)
Yani 2a=a+a ve 3a=2a+a
Aynı şekilde, üs alma işlemi çarpma üstünden tanımlanabilir: ab = ab-1a (b>0 ise)
Yani a²=aa ve a³=a²a
Toplama için artı işareti kullanıldığı halde, standart cebirde çarpma için bir sembol çoğu zaman gerekmez. 12a ifadesi a'nın 12 katını gösterir. Ancak iki sabit sayıyı çarpmak gerektiğinde araya nokta (⋅) ya da çarpı (×) koymak gerekir: 12×5 gibi...
Çıkarma işlemini toplamanın tersi olarak tanımlayalım: 7−4=3 çünkü 7=3+4
Ama 4−7 işlemine gelince, "4'ten 7 çıkmaz" diyoruz çünkü 4<7.
Benzer bir şekilde, 2×5=10 olduğundan, 10/5=2 ama "10 sayısı 3'e bölünmez" diyoruz doğal sayılar kümesinde.
Negatif Sayılar
Doğal sayılara yapacağımız ilk ekleme çıkarma işlemini genelleştirmemizi sağlıyor. Öyle bir m sayısı "icat edelim" ki 1+m=0 olsun. Bu m sayısı doğal değil, çünkü m hiçbir kümenin eleman sayısı olamaz. Peki m sayısı ne işe yarar?
Her doğal sayıdan önceki sayıyı ve sonraki sayıyı kolayca bulabiliriz -- sıfır hariç. "Sıfırdan önceki sayı m olsun" varsayımı ile m'yi ve m'nin katlarını N kümesine eklersek Z (tamsayılar) kümesine ulaşırız.
Tanım denklemini 2 ile çarpınca (1+m)2=2+m2=0 buluyoruz. O halde m2 (m'nin 2 katı) sayısı 2'nin toplamaya göre tersi, yani negatifi olur. Bunu −2 olarak gösterince negatif sayıları tanımlamış olduk.
Tanım denklemini m ile çarpınca (1+m)m=m+m²=0 buluyoruz. Bu denklemin iki tarafına 1 ekleyince 1+m+m²=1 ya da m²=1 özelliğini cebirsel işlemlerle kanıtlarız.
Yukarıda söz konusu olan 4−7 işlemini 4+m7 olarak tanımlayıp m7=m(4+3)=m4+m3 özelliğini kullanarak 4−7=4+m4+m3=m3 yani −3 sonucunu buluruz.
Kesirli Sayılar
Çıkarma işlemini genelleştirmek için bir tek m sayısı ve m'nin katları yeterli olmuştu. Çarpmanın ters işlemi olarak bölmeyi genelleştirmek için her tamsayının tersine ve bunların katlarına ihtiyaç var: 3'ün tersi: 1/3, bunun 10 katı: 10/3
Böylece 10 bölü 3 işleminin sonucunu 10/3 sayısı olarak tanımlayabiliriz. p=a/b kesirli sayısında a bir tamsayı (pozitif, sıfır, negatif olabilir), paydadaki b ise pozitif doğal sayı olmak zorunda.
Eşitleme, sıralama, toplama, çarpma ve ters eleman aşağıdaki tabloda tanımlanıyor:
Her kesir için 2/3=10/15=30/45 gibi sınırsız sayıda gösterim var.
Doğal sayılar için de durum aynı: 7/1=35/5=105/15
0/b şeklindeki kesirler, doğal sıfırın özelliklerini taşıdığı için 0 olarak yazılır.
b/b şeklindeki kesirler, doğal birin özelliklerini taşıdığı için 1 olarak yazılır.
Verilen bir p sayısının negatifi, tamsayılarda olduğu gibi −p ile gösterilir ve p+(−p)=0 özdeşliğini sağlar. Negatifi kendisine eşit olan tek sayı sıfırdır. Verilen bir p sayısının tersi, p-1 ile gösterilir ve p(p-1)=1 özdeşliğini sağlar. p=a/b sayısının tersi, a=0 durumunda tanımsızdır. Sıfır değilse, tanım gereği mesela 8'in tersi 1/8, −3/5'in tersi −5/3 olarak bulunur. Tersi kendisine eşit olan tek sayı birdir.
Kesirli sayıları da ekleyince Q (rasyonel sayılar) kümesine ulaşmış olduk. Rasyonel sayılar kümesinde dört işlemi eksiksiz tanımlamış olduk. Bilgisayarların kullandığı aritmetik de rasyonel olduğuna göre, bütün sayısal uygulamalar bu kümenin içindedir denilebilir.
İrrasyonel Sayılar
Uygulamayı etkilemeyen, ama matematikçileri rahatsız eden önemli bir sorun kaldı: Kenarları birim uzunluktaki eşkenar üçgenin yüksekliğini ya da karenin köşegenini rasyonel sayı olarak yazamazsınız. Başka bir deyişle, 2'nin ya da 3'ün kare kökü iki tamsayının oranı değildir!
Üstelik bu sorun kare köklerle sınırlı değil. Bütün rasyonel sayıların bütün köklerini eklesek bile, aralarında sonsuz irrasyonel sayı kalıyor.
Sanal Sayılar
Yolculuğumuzun son durağında bir sayı türü daha gerekecek. Negatif sayıları göstermek için 1+m=0 şartını sağlayan bir tek sayı icat etmek yeterli olmuştu. Sanal sayılara geçmek için de i²=m şartını sağlayan bir i sayısı gerekiyor -- gerisi düz cebir:
Doğal sayılara negatif sayıları ekleyerek tamsayılara,
kesirli sayıları ekleyerek rasyonel sayılara,
irrasyonel sayıları ekleyerek reel sayılara,
sanal sayıları ekleyerek kompleks sayılara ulaşmış olduk.
Sayılar dünyasındaki seyahat burada bitiyor, çünkü bütün cebirsel denklemleri bu sayılarla çözebiliyoruz. Denklem çözmek için başka bir sayı türü gerekmiyor.
Ödev
1. z=5+12i sayısının iki kare kökünü
a) (x+iy)²=z eşitliğinden iki denklem yazarak,
b) polar koordinatlar kullanarak bulun
2. Bir'in dördüncü köklerini bulun
(z⁴=1 denkleminin 4 farklı kökü var)
3. Google and Wolfram'a "log(-1)" sorunca farklı cevaplar geliyor:
www.wolframalpha.com/input/?i=log+(-1)
www.google.com/search?q=log(-1)
Hangisi doğrusu?
Referans
https://www.wikiwand.com/en/Number
http://www.feynmanlectures.caltech.edu/I_22.html
Kare Kök
kök 2nin anlamı
kompleks kökler
Newton'un iki metodu

Ödev
* Read Newton's generalised binomial theorem
* Apply the theorem to approximate sqrt(1+x) for small x
using another worksheet similar to exp()
* Study the attached table that calculates sqrt(2), e, and π
using methods discovered by Newton 300 years ago
(note that there are 3 separate sheets)
Referans
kompleks kökler
Newton'un iki metodu

Ödev
* Read Newton's generalised binomial theorem
* Apply the theorem to approximate sqrt(1+x) for small x
using another worksheet similar to exp()
* Study the attached table that calculates sqrt(2), e, and π
using methods discovered by Newton 300 years ago
(note that there are 3 separate sheets)
Referans
Binom Teoremi
Verilen bir kümenin alt kümelerinin sayısını bulalım. Mesela, { a, b, c } kümesinin 8 adet alt kümesi olduğunu cebir yardımı ile görebiliriz:
(1+a)(1+b)(1+c) = 1 + a+b+c + ab+ac+bc + abc
Sağdaki 8 terimi eleman sayısına göre gruplayınca, 0 elemanlı bir tek boş küme, 1 elemanlı üç küme, 2 elemanlı üç küme ve 3 elemanlı bir küme olduğu hemen görünüyor. Pascal üçgeninin 3. satırındaki 1-3-3-1 dizisini bulduk.
a = b = c eşitlik durumunda elemanlar arasındaki ayırım kalkar ve
Matematikte "n elemanın k'lı alt kümeleri sayısı" çok sık geçtiği için, bu ifadeye özel bir notasyon bulmuşlar. İki parantez arasında n ve k sayılarını alt alta gösteren bu notasyonu kullanınca, aynı denklem şu şekli alır:
Böylece, binom teoreminin n=3 için özel halini elde ettik. Teoremin genel hali ise:
a≪1 halinde, toplamın ilk birkaç terimi yeterli olacaktır:
a = 1 özel halinde ise, alt kümelerin toplam sayısının 2^n olduğu hemen bulunur.
(1+a)(1+b)(1+c) = 1 + a+b+c + ab+ac+bc + abc
Sağdaki 8 terimi eleman sayısına göre gruplayınca, 0 elemanlı bir tek boş küme, 1 elemanlı üç küme, 2 elemanlı üç küme ve 3 elemanlı bir küme olduğu hemen görünüyor. Pascal üçgeninin 3. satırındaki 1-3-3-1 dizisini bulduk.
a = b = c eşitlik durumunda elemanlar arasındaki ayırım kalkar ve
(1+a)³ = 1 + 3a + 3a² + a³
Matematikte "n elemanın k'lı alt kümeleri sayısı" çok sık geçtiği için, bu ifadeye özel bir notasyon bulmuşlar. İki parantez arasında n ve k sayılarını alt alta gösteren bu notasyonu kullanınca, aynı denklem şu şekli alır:
Böylece, binom teoreminin n=3 için özel halini elde ettik. Teoremin genel hali ise:
a≪1 halinde, toplamın ilk birkaç terimi yeterli olacaktır:
(1+a)^n = 1 + na + n(n-1)a²/2 + . . .
a = 1 özel halinde ise, alt kümelerin toplam sayısının 2^n olduğu hemen bulunur.
Temel Fonksiyonlar
Bu bölümde temel dört analitik fonksiyonun (exp, log, sin, cos) aynı kaynaktan türetildiğini vurgulamak istiyorum. Diyelim ki bir matematik öğrencisi temel analiz konularını, özellikle limit ve türev kavramlarını, teorik olarak çalışmış, fakat bu dört fonksiyonu hiç görmemiş olsun. Çok basit bir tek varsayımla, bu fonksiyonların bütün özellikleri kanıtlanabilir mi?
Temel varsayım şu: Öyle bir e(x) fonksiyonu arıyoruz ki her noktadaki türevi kendisine eşit ve 0 noktasındaki değeri 1 olsun.

Euler sayısı -- ondalık ve kesirli hesap
Euler formülü -- karmaşık sayılar
sin() ve cos() fonksiyonları, pi sayısı
Logaritma
Ödev
1. Excel ya da benzeri bir programla e(x) fonksiyonunu yaklaşık olarak hesaplatın. Negatif x değerleri için yakınsamanın yavaş olduğuna dikkat edin. Bu sorunu nasıl çözersiniz?
2. Metinde geçen c(x) ve s(x) fonksiyonlarını aynı şekilde hesaplatın. Trigonometrik fonksiyonlarla aynı değeri hesapladığını gösterin. Özel iki değer x=π ve x=π/2 için yakınsama nasıl?
3. Euler sayısının hesabında kullanılan limiti genelleştirin (1+a/n) ^n --> e(a)
4. Eymen'in sınavda bir soruyu doğru cevaplama olasılığı 9/10 olsun. 10 soruluk bir sınavda 10 doğru olasılığı nedir? n soruluk sınavda bir soruyu doğru yapma olasılığı (n–1)/n ise, sınavın tamamını doğru yapma olasılığı (1–1/n)^n hangi sayıya yakınsar?
(Eski bir öğrencim Onur Karadeli'nin katkısı)
Referans
http://mathworld.wolfram.com/RootofUnity.html
Temel varsayım şu: Öyle bir e(x) fonksiyonu arıyoruz ki her noktadaki türevi kendisine eşit ve 0 noktasındaki değeri 1 olsun.

Euler sayısı -- ondalık ve kesirli hesap
Euler formülü -- karmaşık sayılar
sin() ve cos() fonksiyonları, pi sayısı
Logaritma
Ödev
1. Excel ya da benzeri bir programla e(x) fonksiyonunu yaklaşık olarak hesaplatın. Negatif x değerleri için yakınsamanın yavaş olduğuna dikkat edin. Bu sorunu nasıl çözersiniz?
2. Metinde geçen c(x) ve s(x) fonksiyonlarını aynı şekilde hesaplatın. Trigonometrik fonksiyonlarla aynı değeri hesapladığını gösterin. Özel iki değer x=π ve x=π/2 için yakınsama nasıl?
3. Euler sayısının hesabında kullanılan limiti genelleştirin (1+a/n) ^n --> e(a)
4. Eymen'in sınavda bir soruyu doğru cevaplama olasılığı 9/10 olsun. 10 soruluk bir sınavda 10 doğru olasılığı nedir? n soruluk sınavda bir soruyu doğru yapma olasılığı (n–1)/n ise, sınavın tamamını doğru yapma olasılığı (1–1/n)^n hangi sayıya yakınsar?
(Eski bir öğrencim Onur Karadeli'nin katkısı)
Referans
http://mathworld.wolfram.com/RootofUnity.html
Süreklilik
Temel derslere geri dönüp bakınca, lisans eğitiminde bazı konuları iyice anlamadan geçtiğimiz ortaya çıkıyor. Süreklilik de böyle bir kavram. Birkaç örnekle anlatmaya çalışacağım.
xn-1 fonksiyonunun türevi her n için tanımlı. Ama iş türevin tersine gelince, 1/x için belirsiz integral beklenmedik şekilde logaritma çıkıyor. Acaba neden n=0 farklı bir rejim? Bu farklı davranış xn fonksiyonundan türetilebilir mi?
xn-1 fonksiyonunun 1'den herhangi bir pozitif a sayısına kadar integrali için iki farklı formül var:
f(a, n) n'nin sürekli bir fonksiyonu ise, n parametresi sıfıra yaklaşırken iki ifadenin eşit olması gerekir:
Bu şekilde yazınca hiç de şaşırtıcı değil, çünkü bu ifade, ax fonksiyonunun x = 0 noktasındaki türevi! Yani xn fonksiyonundan başlayıp ax fonksiyonunun türevi ile logaritmaya ulaşmış olduk.
İkinci örneğimiz analitik geometriden:
y² = 1 + ax² y ≥ 0, −1 ≤ x≤ 0
fonksiyonu a>0 için hiperbol, a<0 için elips tanımlar.
a=0 durumunda konik yerine y=1 doğrusu çıkar.
Peki, a sıfıra (her iki yönden) yaklaşırken ne olur?
Küçük x değerleri için, yaklaşık olarak bir parabol bulduk.
Üçüncü örnek basit bir diferansiyel denklem: y' + y = e-kt, y(0) = 8
Bu denklemi sağlayan y(t) fonksiyonu için iki ayrı çözüm şekli var:
a) k = 1 ise çözüm üstel fonksiyonun lineer bir ifade ile çarpımı:
y(t) = e-t (8 + t)
b) k = 1 değilse çözüm iki farklı üstel fonksiyonun toplamı:
y(t) = A e-t + B e-kt
Çok farklı iki ifade bulduk ama k parametresi 1'e yaklaşırken iki çözümün yaklaşık eşit olması gerekir. Mesela k = 1.01 için, A ve B katsayıları denklemden ve başlangıç şartından bulunabilir:
y(t) = 108 e-t − 100 e-1.01t
Bu ifade şöyle yazılırsa (a) çözümüne yakın olduğu görülür:
y(t) = 8 e-t + 100 e-t (1 − e-0.01t)
Burada e-0.01t yerine yaklaşık değeri olan 1 − 0.01t koyunca yukarıdaki (a) çözümüne hemen ulaşılır.
Aynı sonuç, e-xt fonksiyonunun x = 1 noktasındaki türevi olarak da bulunabilir. Yani e-xt fonksiyonunun t'ye göre türevinden başlayıp aynı fonksiyonun x'e göre türevine ulaşmış olduk.
Ödev
1. ax² − 4x + 20 = 0 denkleminin a≠0 için çözümlerinden birinin, a sıfıra yaklaşırken 5 değerine yaklaştığını gösterin
2. c parametresine bağlı olarak şu denklemin üç ayrı çözüm şekli var:
y'' + 2y' + cy = 0, y(0) = 2, y'(0) = 0
a) c=1.00 ise y(t) = 2 e-t (1 + t)
b) c=0.99 ise y(t) = 11 e-0.9t − 9 e-1.1t
c) c=1.01 ise y(t) = 2 e-t (cos 0.1t + 10 sin 0.1t)
(b) ve (c)deki iki farklı fonksiyonun t≪1 için (a) fonksiyonuna yaklaştığını gösterin
Referans
Bu yazının aslı, birkaç ay önce Damlalar: Süreklilik olarak yayınlanmıştı
xn-1 fonksiyonunun türevi her n için tanımlı. Ama iş türevin tersine gelince, 1/x için belirsiz integral beklenmedik şekilde logaritma çıkıyor. Acaba neden n=0 farklı bir rejim? Bu farklı davranış xn fonksiyonundan türetilebilir mi?
xn-1 fonksiyonunun 1'den herhangi bir pozitif a sayısına kadar integrali için iki farklı formül var:
f(a, n) n'nin sürekli bir fonksiyonu ise, n parametresi sıfıra yaklaşırken iki ifadenin eşit olması gerekir:
İkinci örneğimiz analitik geometriden:
y² = 1 + ax² y ≥ 0, −1 ≤ x≤ 0
fonksiyonu a>0 için hiperbol, a<0 için elips tanımlar.
a=0 durumunda konik yerine y=1 doğrusu çıkar.
Peki, a sıfıra (her iki yönden) yaklaşırken ne olur?
Küçük x değerleri için, yaklaşık olarak bir parabol bulduk.
Üçüncü örnek basit bir diferansiyel denklem: y' + y = e-kt, y(0) = 8
Bu denklemi sağlayan y(t) fonksiyonu için iki ayrı çözüm şekli var:
a) k = 1 ise çözüm üstel fonksiyonun lineer bir ifade ile çarpımı:
y(t) = e-t (8 + t)
b) k = 1 değilse çözüm iki farklı üstel fonksiyonun toplamı:
y(t) = A e-t + B e-kt
Çok farklı iki ifade bulduk ama k parametresi 1'e yaklaşırken iki çözümün yaklaşık eşit olması gerekir. Mesela k = 1.01 için, A ve B katsayıları denklemden ve başlangıç şartından bulunabilir:
y(t) = 108 e-t − 100 e-1.01t
Bu ifade şöyle yazılırsa (a) çözümüne yakın olduğu görülür:
y(t) = 8 e-t + 100 e-t (1 − e-0.01t)
Burada e-0.01t yerine yaklaşık değeri olan 1 − 0.01t koyunca yukarıdaki (a) çözümüne hemen ulaşılır.
Aynı sonuç, e-xt fonksiyonunun x = 1 noktasındaki türevi olarak da bulunabilir. Yani e-xt fonksiyonunun t'ye göre türevinden başlayıp aynı fonksiyonun x'e göre türevine ulaşmış olduk.
Ödev
1. ax² − 4x + 20 = 0 denkleminin a≠0 için çözümlerinden birinin, a sıfıra yaklaşırken 5 değerine yaklaştığını gösterin
2. c parametresine bağlı olarak şu denklemin üç ayrı çözüm şekli var:
y'' + 2y' + cy = 0, y(0) = 2, y'(0) = 0
a) c=1.00 ise y(t) = 2 e-t (1 + t)
b) c=0.99 ise y(t) = 11 e-0.9t − 9 e-1.1t
c) c=1.01 ise y(t) = 2 e-t (cos 0.1t + 10 sin 0.1t)
(b) ve (c)deki iki farklı fonksiyonun t≪1 için (a) fonksiyonuna yaklaştığını gösterin
Referans
Bu yazının aslı, birkaç ay önce Damlalar: Süreklilik olarak yayınlanmıştı
Cebirin Temel Teoremi
Karmaşık sayıları burada kullanalım

Ödev
* Study: Poly roots.xls (attached)
Watch the demo by Murat Bilsel:
youtube.com/watch?v=epx1S5oh8dM
* Make a similar worksheet using Matlab, Excel, etc
start with 3 or 4 roots (at least one complex root)
determine your polynomial f(z) with given roots
plot the behavior of f(z) as |z| grows
[ipucu: önce kökleri seçin, ordan polinomu bulun]
Referans

Ödev
* Study: Poly roots.xls (attached)
Watch the demo by Murat Bilsel:
youtube.com/watch?v=epx1S5oh8dM
* Make a similar worksheet using Matlab, Excel, etc
start with 3 or 4 roots (at least one complex root)
determine your polynomial f(z) with given roots
plot the behavior of f(z) as |z| grows
[ipucu: önce kökleri seçin, ordan polinomu bulun]
Referans
- cut-the-knot.org/fta/fta_sketch1.shtml
- mathworld.wolfram.com/FundamentalTheoremofAlgebra.html
Integral ve Türev
F'(x) = f(x)

Ödev
* Select a function F(x) and evaluate its analytical derivative f(x)
* Demonstrate numerically that f(x) = F'(x) at some fixed point x=b
using table and chart in Excel or similar software
* Demonstrate numerically that the area under f(x) from a to b
is F(b)–F(a), for some fixed a and b
Referans

Ödev
* Select a function F(x) and evaluate its analytical derivative f(x)
* Demonstrate numerically that f(x) = F'(x) at some fixed point x=b
using table and chart in Excel or similar software
* Demonstrate numerically that the area under f(x) from a to b
is F(b)–F(a), for some fixed a and b
Referans
Algoritmalar
GCD
MST
Subsets
Partition
TSP

Ödev
Referans
http://www.americanscientist.
MST
Subsets
Partition
TSP

Ödev
given: 50 numbers with sum B
final static int[] A
= {12913, 13603, 14135, 15215, 16692, 17762, 18974, 20088, 20138,
20188, 21250, 24296, 24444, 25428, 25976, 27792, 28038, 31170,
31338, 32752, 34102, 35614, 37556, 39618, 40556, 41880, 42444,
43852, 44004, 46016, 48172, 50334, 50494, 51792, 53138, 53530,
53692, 56370, 56560, 59536, 60428, 62032, 62850, 62928, 66382,
68084, 68416, 69276, 69824, 70414};
find: a subset of these numbers with sum B/2 = 1021043
Referans
http://www.americanscientist.
Kaydol:
Kayıtlar (Atom)