3-4-5 Üçgeni

Arazide dik üçgen yapmak için çok basit bir gönye kullanılır: Kenarlarları 3-4-5 sayılarının katı olan bir üçgen. Aritmetik $3^2 + 4^2 = 5^2$ ve Pisagor teoremi bu üçgenin dik açılı olduğunu söylüyor.

https://tr.pinterest.com/pin/436286282625753185/

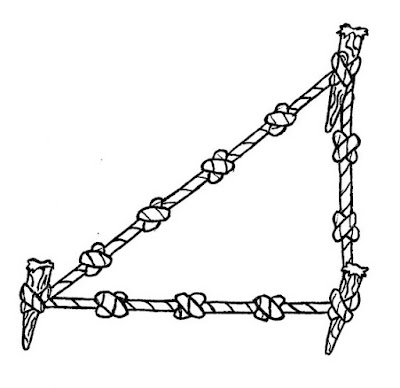
Bu üçgeni kağıttan katlamanın birkaç yolunu okumuştum. Bu sabah gördüğüm çok basit bir yöntem (Kazuo Haga) hepsinden daha kolay. Kare kağıdın A köşesini üst kenarın orta noktasına getirip katlayınca üç adet 3-4-5 üçgeni elde edilir: (daha güzel bir yöntem yazının sonunda)

Kenar uzunluğunu 1 (bir) alarak yukarıda gösterilen uzunluklar kolayca hesaplanır. Yan ürün olarak, alt kenarı altıda bir ve sağ kenarı üçte bir oranında (C noktasında) bölmüş oluruz. 

Genel Formül

Bir problemi çözen matematikçi asla o sonuçla yetinmez. Çözümü daha kısa, daha güzel ve daha genel yapmaya uğraşır. Bu problem, A köşesini üst kenarın ortasına değil, herhangi bir yerine getirmek şeklinde genellenebilir:

A köşesini sol üst köşeden b uzaklığına getirip katlayınca, şekilde görülen x ve y değerleri nasıl hesaplanır? Yani, katlama sonunda sol ve sağ kenarlarda ortaya çıkan B ve C noktalarının alt kenara uzaklığını bulmak istiyoruz. Şekildeki en önemli ayrıntı, katlamanın gereği olarak AB = $x$ uzunluğunun sol tarafta iki kere çizilmiş olması. (Sağdaki üçgende aynı özellik geçerli değil)

Soldaki dik üçgende $(1-x)^2 + b^2 = x^2$  eşitliğini kullanarak

hipotenüs $x = (1+b^2)/2$  ve

dik kenar $1-x = (1-b^2)/2$ bulunur.

Soldaki ve sağdaki üçgenlerin benzerliğini dik kenarlara uygularsak,

$$ \frac {b}{1-y} = \frac {1-x}{1-b} = \frac {1+b}2 $$

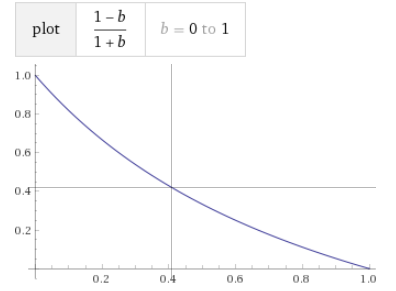
ve buradan $y = \frac {1-b}{1+b}$ sonucuna ulaşırız. 

Özel halde, $b=1/2$ verildiğinde $y=1/3$ bulunur.

Çözüm: $f(b) = (1−b)/(1+b)$  fonksiyonun $0<b<1$ aralığındaki grafiği aşağıda

f(b) fonksiyonu

Pisagor Üçlüleri  

Tanım: $a^2 + b^2 = c^2$  denklemini sağlayan tamsayılar

Konu başlığındaki 3-4-5 üçgeni ne oldu? Açılar değiştiği için her $b$ değeri farklı bir dik üçgen verir. Üstelik $b$ rasyonel bir sayı ise, hesaplanan değerler de rasyonel olacağından, ortak payda ile çarpıldığında bütün kenarlar tamsayı olur ve tanım gereği Pisagor üçlüleri elde edilir. Verilen $b$ sayısından $x$ ve $y$ değerlerini kesir olarak hesaplayan şu sayfanın ürettiği birkaç örneği aşağıda ekledim. Pisagor üçlülerinin ne kadar çok olduğunu bu sayfada görebilirsiniz.

https://maeyler.github.io/JS/math/Folding.html

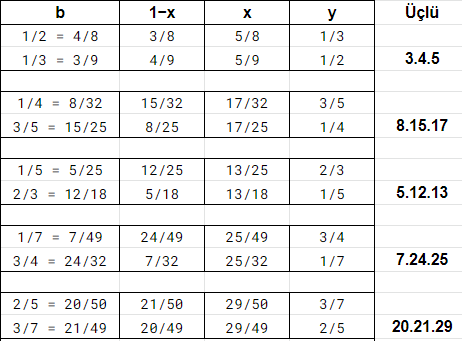b değerinden hesaplanan x, y ve Pisagor üçlüsü

Verilen bir Pisagor üçlüsünden de rasyonel $b$ ve $y$ değerleri kolayca bulunur.

Yine Euclid!

Bu tablodaki kesirlerin basitliğini merak ettim. Küçük tamsayılarla yapılan kesirlerin sonucunda, formüller çok basit olmadığı halde, yine küçük tamsayılar çıkıyor, acaba neden? 

Konuyu araştırınca, az bilinen başka bir Euclid formülü çıktı. 

$b = n/m \quad (m>n>0)$ rasyonel sayısı ile başlarsak, soldaki üçgenin kenarları şöyle çıkıyor:

$b = 2mn/p,  1-x = (m^2-n^2)/p,  x = (m^2+n^2)/p$

(ortak payda $p = 2m^2$)  ve  $y = (m-n)/(m+n)$

Paydalar eşitlendiği için, üç kesrin payları aranan üçlüyü verir:

$(2mn, m^2-n^2, m^2+n^2) \Rightarrow $ $(2mn)^2 + (m^2-n^2)^2 = (m^2+n^2)^2$

Bu şekilde bulunan sayıların Pisagor üçlüsü olduğunu göstermiş olduk. Fazlası, bütün Pisagor üçlülerinin Euclid formülüne uyduğu aşağıdaki linkte [4] kanıtlanmış.

It is a fascinating thought that this chapter could have been written while Euclid was looking over my shoulder.

"Bu bölüm, Euclid omuzumun üstüden izlerken yazılabilirdi" düşüncesi büyüleyici...

E W Dijkstra (1976), A Discipline of Programming, Prentice-Hall, p. 6

Aynen öyle, bu bölüm (notasyon ve yazılım hariç) 2300 sene önce yazılabilirdi...

Ödev

1. Hipotenüsü AB olan dik üçgende, Pisagor teoremini kullanarak AB uzunluğunu bulun

2. C köşesindeki küçük üçgenin 3-4-5 oranında olduğunu sayılarla doğrulayın

3. BC uzunluğunu hesaplayın ve ABC üçgeninin de diğerlerine benzer olduğunu gösterin

4. $f(b)$ fonksiyonunun tersinin kendisi olduğunu gösterin ve $f(x) = x$ denklemini sağlayan sabit noktasını bulun

5. Yukarıda görülmeyen $(9, 40, 41)$ Pisagor üçlüsü için iki adet $b$ değeri bulun (neden iki?)

Referans

1. Kare kağıdı üç eşit parçaya bölmek

https://www.matematiksel.org/kare-bir-kagidi-3e-katlayabilir-misiniz/

2. Aynı konu, İngilizce

https://plus.maths.org/content/folding-numbers

3. Yazının konusu olan 3-4-5 üçgeni hakkında

https://www.mathopenref.com/triangle345.html

4. Pisagor üçlüsü, tanımı ve özellikleri

https://en.wikipedia.org/wiki/Pythagorean_triple

5. f(b) değerini kesir olarak hesaplayan JS sayfamız

https://maeyler.github.io/JS/math/Folding.html

Daha basit bir yöntem (Eylul 2021)

3-4-5 üçgenini 4x4 kareden elde etmek için iki kere katlamak yeterli:

Matematikte "en iyiyi buldum" diyemezsiniz!

Çarpışan Toplar

Görsel benzetimin yaygınlaşması, Corona salgının yan etkilerinden biri oldu. Hastalığın nasıl bulaşacağını ve izolasyonun etkisini tahmin eden inandırıcı benzetimlerle tanıştık. Aynı günlerde ilk referanstaki sayfayı buldum. Çarpışma modeli eksikti ama topların gösterimi çok başarılıydı.

Söz konusu yazılımın evrimini anlatırken, toplam kinetik enerjinin sabit kaldığı esnek çarpışma varsayımını kullanacağız. Momentumun korunumu da en temel mekanik kuralı...


Tek boyutlu çarpışma

Eşit kütleli iki top doğru bir hat üstünde çarpışırsa iki topun hızı yer değiştirir. Bilardo masasından bir örnek verelim: Hareketsiz duran bir topa tam ortasından çarpan ikinci top durur ve ilk top aynı hızla harekete geçer. Şimdi bu sonuca denklemlerden ulaşalım:

$v_1, v_2$ topların ilk hızını göstersin. Tek boyutlu hızları modellemek için işaretli sayılar (tek boyutlu vektör) yeterli. Hız pozitif ise top eksen yönünde sağa doğru, negatif ise ters yönde sola doğru hareket ediyor.

Toplam momentum ve enerjinin sabit kaldığı tek çözüm $v'_1 = v_2, v'_2 = v_1$ olarak bulunur, her top diğerinin ilk hızını alır.

Kütleler eşit değilse, işlemler biraz daha uzun sürer ve şu sonuca ulaşılır:

Sonuç şöyle yazılınca hem sağlaması daha kolay olur, hem de genel formülün özel hali olarak okunabilir:

$$ \begin{matrix} v'_1 = v_1 + m_2 k \Delta v, \quad v'_2 = v_2 − m_1 k \Delta v \\[8px] k = 2/(m_1 + m_2), \quad \Delta v = (v_2 − v_1) \end{matrix} $$

Yani, iki top arasındaki hız farkı, diğer topun kütlesi ile orantılı olarak paylaştırılır. Hafif top daha çok hız kazanır. Okuyucu bu çözümün toplam momentum ve enerjiyi değiştirmediğini kolayca sağlayabilir.


İki boyut, eşit kütleler

Daha ilginç çarpışmaları anlamak için ikinci ve üçüncü boyuta geçmek lazım. Vektör yaklaşımı kullanırsak boyut sayısı hiç önemli değil, aynı formüller geçerli. Önce iki eşit kütle ile başlayalım.

İki top dokunduğu anda merkezleri birleştirelim. Hız değişimi sadece bu doğrultuda $(\Delta \mathbf{x})$ gerçekleşir. Buna dik olan hızlar asla değişmez. O halde ilk hızın $\Delta \mathbf{x}$ vektörüne paralel bileşeni (izdüşümü) diğer topa geçecek, dik bileşen ise ilk topta kalacaktır:

Hareketli resimdeki en önemli kare, ilk hızı ve iki bileşenini gösteriyor:

İzdüşüm hesabı lineer cebirin en temel konularından biridir:
$$ \mathbf{a_x} = \frac {\langle\mathbf{a}, \mathbf{x}\rangle}{\langle\mathbf{x}, \mathbf{x}\rangle} \mathbf{x} \quad \textit{projection of } \mathbf{a} \textit{ on } \mathbf{x} $$
Çarpışma problemine uygulayınca, iki topun hız farkının $\Delta \mathbf{x}$ üstüne izdüşümünden şu sonuca varılır:

$$ \begin{matrix} \mathbf{v}'_1 = \mathbf{v}_1 + P \Delta \mathbf{x}, \quad \mathbf{v}'_2 = \mathbf{v}_2 − P \Delta \mathbf{x} \\[8px] P = \frac {\langle\Delta \mathbf{v}, \Delta \mathbf{x}\rangle} {\langle\Delta \mathbf{x}, \Delta \mathbf{x}\rangle} = \langle\Delta \mathbf{v}, \Delta \mathbf{x}\rangle / \lVert \Delta \mathbf{x}\rVert^2 \\[8px] \Delta \mathbf{v} = (\mathbf{v}_2 − \mathbf{v}_1), \quad \Delta \mathbf{x} = (\mathbf{x}_2 − \mathbf{x}_1) \end{matrix} $$

Okuyucu bu olağanüstü basit formülü sağlamalı ve üstünde düşünmelidir. Trigonometri kullanmadan, nasıl olur da iki ve üç boyutta sonuca ulaşır? Formülün büyüsü iki vektörün iç çarpımında gizli olabilir mi?

Önemli not: Vektörlerle çalışırken kinetik enerji koordinatlarla değil, yine iç çarpımla hesaplanır. Elbette trigonometri yardımıyla aynı sonuçlar bulunur, ama hesap süresi daha uzun olur. Enerji hesabı için hız vektörlerinin uzunluğu gerekiyor:

$$ \begin{matrix} \lVert \mathbf{v}'_1\rVert^2 = \lVert \mathbf{v}_1\rVert^2 + 2P \langle \mathbf{v}_1, \Delta \mathbf{x}\rangle + P^2 \lVert \Delta\mathbf{x}\rVert^2 \\[8px] \lVert \mathbf{v}'_2\rVert^2 = \lVert \mathbf{v}_2\rVert^2 - 2P \langle \mathbf{v}_2, \Delta \mathbf{x}\rangle + P^2 \lVert \Delta\mathbf{x}\rVert^2 \end{matrix} $$

Toplam enerjinin sabit kaldığını göstermek için bu iki denklemi toplayıp sadeleştirin...


Genel çözüm

Çok boyutlu genel çözüm formülünü 2. referanstan alalım:

en.wikipedia.org/wiki/Elastic_collision

Karmaşık görünen bu çözüm şöyle yazılınca epeyce basitleşir:

$$ \begin{matrix} \mathbf{v}'_1 = \mathbf{v}_1 + m_2 k P \Delta \mathbf{x} \\[8px] \mathbf{v}'_2 = \mathbf{v}_2 − m_1 k P \Delta \mathbf{x} \\[8px] k = 2/(m_1 + m_2), \quad P = \langle\Delta \mathbf{v}, \Delta \mathbf{x}\rangle / \lVert \Delta \mathbf{x}\rVert^2 \\[8px] \Delta \mathbf{v} = (\mathbf{v}_2 − \mathbf{v}_1), \quad \Delta \mathbf{x} = (\mathbf{x}_2 − \mathbf{x}_1) \end{matrix} $$

Bu genel çözümün iki farklı özel halini yukarıda incelemiştik:
1. Vektör yerine skalar $(P \Delta x = \Delta v)$ kullanırsak, formül tek boyuta indirgenir.
2. Eşit kütleler haline indirgemek için $m \text{ ve } k$ değerlerini silmek yeterli $(mk = 1)$.

$$ \begin{matrix} \textit{Tek boyut} & \textit{Eşit kütleler} \\ v'_1 = v_1 + m_2 k \Delta v & \mathbf{v}'_1 = \mathbf{v}_1 + P \Delta \mathbf{x} \\ v'_2 = v_2 − m_1 k \Delta v & \mathbf{v}'_2 = \mathbf{v}_2 − P \Delta \mathbf{x} \\[10px] k = 2/(m_1 + m_2) & \quad P = \langle\Delta \mathbf{v}, \Delta \mathbf{x}\rangle / \lVert \Delta \mathbf{x}\rVert^2  \end{matrix} $$

Yazılımın ana hatları

Çarpışan iki top b2 ve b1 olsun. Topların yeri, hızı, kütlesi:

  x2 = b2.pos,  x1 = b1.pos
  v2 = b2.vel,  v1 = b1.vel
  m2 = b2.size, m1 = b1.size

Çarpışma sonrası hızların hesabı şöyle yapılır:

  let dx = b2.pos.minus(b1.pos) // x2-x1
  let dv = b2.vel.minus(b1.vel) // v2-v1
  let m  = b1.size + b2.size    // m1+m2
  let kP = (2/m)*dv.inner(dx)/dx.inner(dx)
  b1.vel.add(+kP*b2.size, dx)
  b2.vel.add(-kP*b1.size, dx)

Bu formülü uygulamadan önce, iki topun tam dokunduğuna emin olmak gerekir. Benzetim sırasında zaman sürekli akmadığı için, çarpışmayı fark ettiğimizde iki top birbirinin içine girmiş olabilir. Dokunma zamanını hesaplayıp tam o andaki koordinatları kullanmak gerekiyor.

  let a = dv.inner(dv)  // |Δv|²
  if (a < 0.0001) continue //same velocity
  let b = dv.inner(dx)/a // <Δv,Δx>/<Δv,Δv>
  let c = (dx.inner(dx) - m*m)/a
  //solve t² + 2b*t + c = 0
  if (b*b < c) continue //no real solution 
  if (1+2*b+c > 0) continue //solution t>1
  let tt = (-b-Math.sqrt(b*b-c))
  b1.update(tt); b2.update(tt)

Uygulamadaki en önemli zorluk, topların sayısı artınca ortaya çıkıyor. Aynı zaman aralığında bir top iki topa birden çarparsa, iki çarpışmayı zaman sırasında ayrı ayrı ele almak gerekiyor. Aynı aralıkta ikiden fazla çarpışma olursa basit formüller hata veriyor ve süreksiz bir hareket gözleniyor. Top sayısının girildiği kutunun rengi (beyazdan sarı ve kırmızıya) bu durumun işareti: Temel varsayımın ihlali nedeniyle benzetim doğru çalışmıyor. Top sayısını azaltmak gerekecek. (Formülün ilginç bir sonucu olarak, toplam enerjinin bu halde bile korunduğunu gözledik)





Doğrulama (validation)

Her benzetim çalışmasının doğrulanması gerekir. (Ref: Osman Balcı) Bu yazılımda iki doğrulama aracı kullandım:

1. Toplam enerji on binlerce çarpışma sonunda aynı kalıyor, o halde esnek çarpışmalar doğru modellenmiş (Dev Tools'da total() yazarak bunu görebilirsiniz)

2. Görsel doğrulama. Programın ilk sürümünde ilginç hatalar gözledik:
* toplar birbirine kenetlenip dönüyordu
* görünen topların sayısı zamanla azalıyordu
* ekranın kenarlarına takılıp kalan toplar vardı
Bunların hepsi yukarıda anlatılan hassas zaman hesabı ile düzeltildi


Referans

1. Mozilla eğitim sayfalarında uygulamanın temelini buldum (bu modelde toplar birbirinin içinden geçerken sadece renk değiştiriyor, hızları aynı kalıyor)

2. Genel anlatım ve çözüm formülü Wikipedia'da:
https://en.wikipedia.org/wiki/Elastic_collision

3. Esnek çarpışmaları vektörlerle modelleyen bir makale ve Bouncescope uygulaması:
http://www.vobarian.com/collisions/

4. Yazılım sayfası:
https://maeyler.github.io/JS/canvas/colliding